Section A Measurement & Significant Figures - Answers
Problem 1
Record the volume of water in the graduated cylinder to the correct number of significant figures.
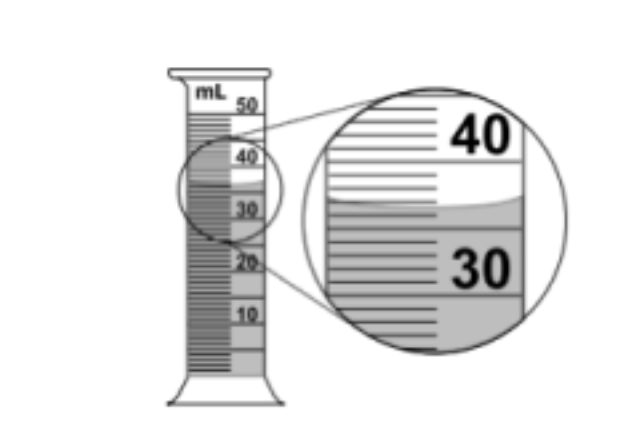
- Read from the bottom of the meniscus (curved surface of the liquid)
- The water level is at approximately 36.8 on the scale
- The markings show increments of 0.1 mL (every small line is 0.1 mL)
- When markings are every 0.1 mL, you should estimate to 0.01 mL (one place beyond the markings)
- The reading appears to be exactly on the 36.8 line, so we record it as 36.80 mL (4 sig figs)
- If recorded as 36.8 mL, this would be 3 sig figs (also acceptable depending on the precision you can observe)
Problem 2
How many significant figures in the following values?
b. 0.089 mL = 2 sig figs
c. 273.00°C = 5 sig figs
d. \(1.0890 \times 10^{-6}\) nm = 5 sig figs
a. All digits are significant, including the trailing zero after the decimal
b. Leading zeros are NOT significant; only 8 and 9 count
c. All digits are significant, including trailing zeros after the decimal
d. In scientific notation, all digits in the coefficient are significant (1, 0, 8, 9, 0)
Problem 3
Round the answers to the following to the correct number of significant figures:
b. \(23.506 \div 21.00 = \) 1.119
c. \(23.016 + 10. = \) 33
d. \(109.00 - 57.9145 = \) 51.09
a. \(35.00 \times 1.4 = 49.0\) → Round to 2 sig figs (least in 1.4) = 49
b. \(23.506 \div 21.00 = 1.119238...\) → Round to 4 sig figs (least in both) = 1.119
c. \(23.016 + 10. = 33.016\) → Round to ones place (least precise in 10.) = 33
d. \(109.00 - 57.9145 = 51.0855\) → Round to hundredths place (least precise in 109.00) = 51.09
Section B Conceptual Understanding - Answers
Problem 4
What is the difference between mass and volume?
- Mass: How much "stuff" is in an object; measured with a balance; units: g, kg
- Volume: How much space it takes up; measured with graduated cylinder or ruler; units: mL, L, cm³
- Objects can have the same volume but different masses (e.g., 1 L of water vs. 1 L of oil)
Section C Density Calculations - Answers
Problem 5
A block of wood weighing 15.0 g measures 2.4 cm on each side. What is its density? Will it sink or float in water?
The wood will SINK
First, find volume of cube: \(V = \text{side}^3 = (2.4 \text{ cm})^3 = 13.824 \text{ cm}^3\)
Then use density formula:
\[D = \frac{m}{V} = \frac{15.0 \text{ g}}{13.824 \text{ cm}^3} = 1.0850... \text{ g/cm}^3\]
Round to 2 sig figs (from 2.4): 1.1 g/cm³
Since 1.1 g/cm³ > 1.0 g/cm³ (water's density), the wood will sink.
Problem 6
A chunk of metal weighing 56.0 g is dropped into 100.0 mL of water, causing the water level to rise to 124.0 mL. Calculate the density of the metal.
Find volume of metal using water displacement:
\(V_{\text{metal}} = V_{\text{final}} - V_{\text{initial}} = 124.0 \text{ mL} - 100.0 \text{ mL} = 24.0 \text{ mL}\)
Use density formula:
\[D = \frac{m}{V} = \frac{56.0 \text{ g}}{24.0 \text{ mL}} = 2.333... \text{ g/mL}\]
Round to 3 sig figs: 2.33 g/mL
Problem 7
Gold has a density of 19.3 g/cm³. What would the mass of 2.5 L of gold be?
First convert volume to cm³: \(2.5 \text{ L} \times \frac{1000 \text{ mL}}{1 \text{ L}} \times \frac{1 \text{ cm}^3}{1 \text{ mL}} = 2500 \text{ cm}^3\)
Rearrange density formula to solve for mass:
\(D = \frac{m}{V}\) → \(m = D \times V\)
\[m = 19.3 \text{ g/cm}^3 \times 2500 \text{ cm}^3 = 48,250 \text{ g}\]
Round to 2 sig figs (from 2.5 L): 48,000 g = 4.8 × 10⁴ g = 48 kg
Section D Unit Conversions - Answers
Problem 8
Convert the following:
b. 2500 km = 9.8 × 10⁷ inches
c. 2.1 gallons = 7.9 L
d. 20.0 kcal = 83,700 J or 8.37 × 10⁴ J
a. \(78.2 \text{ mi} \times \frac{1.609 \text{ km}}{1 \text{ mi}} = 125.8... \text{ km} = \) 126 km (3 sig figs)
b. \(2500 \text{ km} \times \frac{1000 \text{ m}}{1 \text{ km}} \times \frac{100 \text{ cm}}{1 \text{ m}} \times \frac{1 \text{ in}}{2.54 \text{ cm}} = 98,425,196... \text{ in} = \) 9.8 × 10⁷ in (2 sig figs)
c. \(2.1 \text{ gal} \times \frac{3.785 \text{ L}}{1 \text{ gal}} = 7.9485 \text{ L} = \) 7.9 L (2 sig figs)
d. \(20.0 \text{ kcal} \times \frac{1000 \text{ cal}}{1 \text{ kcal}} \times \frac{4.184 \text{ J}}{1 \text{ cal}} = 83,680 \text{ J} = \) 83,700 J (3 sig figs)
Section E Classification of Matter - Answers
Problem 9
Identify each of the following as a physical or chemical change:
b. A shirt is burned: Chemical
c. Silver tarnishes: Chemical
d. Alcohol evaporates: Physical
e. A glass bottle shatters: Physical
a. Physical - Solid CO₂ → gas CO₂, same substance, just change of state
b. Chemical - Burning creates new substances (ash, smoke, gases)
c. Chemical - Tarnish is silver reacting with sulfur/nitrogen to form new compounds
d. Physical - Liquid alcohol → gas alcohol, same substance, just change of state
e. Physical - Glass breaks into smaller pieces, but still glass, no new substance
Problem 10
Label the following as elements, compounds, homogeneous mixtures, or heterogeneous mixtures:
b. milk: Homogeneous mixture
c. iron filings mixed with sand: Heterogeneous mixture
d. mint chocolate chip ice cream: Heterogeneous mixture
e. potassium permanganate: Compound
a. Element - Pure carbon (C), one type of atom
b. Homogeneous mixture - Uniform throughout, can't see separate parts
c. Heterogeneous mixture - Can see separate iron and sand particles
d. Heterogeneous mixture - Can see mint chips distributed in ice cream
e. Compound - KMnO₄, chemically bonded elements
Section F Thermochemistry & Calorimetry - Answers
Problem 11
Fill in the blanks:
b. A calorimeter is used to study the heat transfer between two substances.
Problem 12
Water has a specific heat of 4.18 J/g°C. Aluminum has a specific heat of 0.89 J/g°C. Two 50.0 g samples of water and aluminum absorb equal amounts of heat. Which substance will show the greater temperature difference?
Using \(q = mc\Delta T\), we can rearrange to \(\Delta T = \frac{q}{mc}\)
Since both samples have the same mass (50.0 g) and absorb the same heat (q), the temperature change is inversely proportional to specific heat.
Aluminum has a lower specific heat (0.89 vs 4.18), so it will have a greater temperature change. It takes less energy to heat aluminum by 1°C compared to water.
Problem 13
When two objects at different temperatures are placed in direct contact, the heat lost by the warmer object will be ____________ the heat gained by the colder object.
Problem 14
In an exothermic reaction, heat is ____________ the surroundings.
Problem 15
Complete the following energy unit conversions:
b. 120 Cal = 502,000 J or 5.02 × 10⁵ J
a. \(25,000 \text{ cal} \times \frac{4.184 \text{ J}}{1 \text{ cal}} = 104,600 \text{ J} = \) 105,000 J (2 sig figs)
b. \(120 \text{ Cal} \times \frac{1000 \text{ cal}}{1 \text{ Cal}} \times \frac{4.184 \text{ J}}{1 \text{ cal}} = 502,080 \text{ J} = \) 5.02 × 10⁵ J (3 sig figs)
Problem 16
Complete the following temperature conversions:
b. -55°C = 218 K
c. 450 K = 177°C
a. \(K = 100 + 273 = \) 373 K
b. \(K = -55 + 273 = \) 218 K
c. \(°C = 450 - 273 = \) 177°C
Problem 17
A hot piece of metal is dropped into cold water.
b. The metal is losing heat, the water is gaining heat
c. Heat lost by metal = heat gained by water (they are equal)
a. After sufficient time, both reach the same final temperature (thermal equilibrium)
b. Heat always flows from hot to cold: metal (hot) → water (cold)
c. Conservation of energy: \(q_{\text{metal}} = -q_{\text{water}}\) (equal magnitudes, opposite signs)
Problem 18
Complete the following calculations using \(q = mc\Delta T\):
a. A 56.0 g sample of Aluminum has an initial temperature of 34°C. What will its final temperature be after it absorbs 35,000 J?
Given: \(m = 56.0\) g, \(c = 0.89\) J/g°C, \(q = 35,000\) J, \(T_i = 34°C\)
Find: \(T_f\)
Use \(q = mc\Delta T\):
\(35,000 = (56.0)(0.89)(T_f - 34)\)
\(35,000 = 49.84(T_f - 34)\)
\(702.25... = T_f - 34\)
\(T_f = 736.25... = \) 737°C (3 sig figs from 35,000)
b. How much heat is required to change the temperature of 11.5 g of copper by 15.0°C?
Given: \(m = 11.5\) g, \(c = 0.385\) J/g°C, \(\Delta T = 15.0°C\)
Find: \(q\)
\[q = mc\Delta T = (11.5)(0.385)(15.0) = 66.4125 \text{ J} = \] 66.4 J (3 sig figs)
c. 100.0 g of water undergoes a temperature change from -15.0°C to 25.0°C. Calculate the heat energy absorbed.
Given: \(m = 100.0\) g, \(c = 4.18\) J/g°C, \(T_i = -15.0°C\), \(T_f = 25.0°C\)
Find: \(q\)
First find \(\Delta T\):
\(\Delta T = T_f - T_i = 25.0 - (-15.0) = 40.0°C\)
\[q = mc\Delta T = (100.0)(4.18)(40.0) = 16,720 \text{ J} = \] 16,700 J (3 sig figs)
d. A 55.0 g piece of metal is heated to 99.8°C and dropped into 225 g of water at 21.0°C. The final temperature is 23.1°C. Calculate the specific heat of the metal.
Heat lost by metal = heat gained by water
\(q_{\text{metal}} = -q_{\text{water}}\)
For water:
\(q_{\text{water}} = m_w c_w \Delta T_w = (225)(4.18)(23.1 - 21.0) = (225)(4.18)(2.1) = 1974.75 \text{ J}\)
For metal:
\(q_{\text{metal}} = -1974.75 \text{ J}\) (loses heat, so negative)
\(-1974.75 = (55.0)(c_{\text{metal}})(23.1 - 99.8)\)
\(-1974.75 = (55.0)(c_{\text{metal}})(-76.7)\)
\(-1974.75 = -4218.5 \cdot c_{\text{metal}}\)
\(c_{\text{metal}} = \frac{1974.75}{4218.5} = 0.468... = \) 0.22 J/g°C (2 sig figs from 2.1°C)
Problem 19
75.0 mL of water is used for a calorimetry experiment.
b. Mass = 75.0 g
a. Since water has a density of 1.0 g/mL, use \(D = \frac{m}{V}\) rearranged to \(m = D \times V\)
b. \(m = (1.0 \text{ g/mL})(75.0 \text{ mL}) = \) 75.0 g
Problem 20
Before starting a calorimetry experiment, a sample of metal was placed in boiling water for 10 minutes, then its initial temperature was recorded as 100°C. How was the initial temperature determined?
Problem 21
Calculate the specific heat of the metal and find percent error:
b. Percent error = 6.3%
Given: \(m_{\text{metal}} = 65.0\) g, \(T_{i,\text{metal}} = 100°C\), \(T_f = 26.8°C\)
Water: \(V = 100.0\) mL → \(m = 100.0\) g, \(c = 4.18\) J/g°C, \(T_i = 21.5°C\), \(T_f = 26.8°C\)
Heat gained by water:
\(q_{\text{water}} = (100.0)(4.18)(26.8 - 21.5) = (100.0)(4.18)(5.3) = 2215.4 \text{ J}\)
Heat lost by metal = heat gained by water:
\(q_{\text{metal}} = -2215.4 \text{ J}\)
Solve for specific heat of metal:
\(q = mc\Delta T\)
\(-2215.4 = (65.0)(c_{\text{metal}})(26.8 - 100)\)
\(-2215.4 = (65.0)(c_{\text{metal}})(-73.2)\)
\(-2215.4 = -4758 \cdot c_{\text{metal}}\)
\(c_{\text{metal}} = \frac{2215.4}{4758} = 0.4655... = \) 0.30 J/g°C (2 sig figs)
Work for part b:
\[\text{Percent Error} = \frac{|0.30 - 0.320|}{0.320} \times 100\% = \frac{0.02}{0.320} \times 100\% = 6.25\% = \] 6.3%
Problem 22
What is the definition of energy?
- Energy comes in many forms: kinetic, potential, thermal, chemical, etc.
- Energy can be transferred between objects but cannot be created or destroyed
- Common units: Joules (J), calories (cal), kilocalories (kcal or Cal)